| |
Własności fynkcji
Dla każdej funkcji możemy podać jej własności. Są nimi:
- dziedzina funkcji
- zbiór wartości funkcji
- miejsca zerowe funkcji
- zbiór tych argumentów, dla których funkcja jest dodatnia
- zbiór tych argumentów, dla których funkcja jest ujemna
- monotoniczność
- najmniejsza i największa wartość funkcji
- różnowartościowość
- parzystość
- nieparzystość
- okresowość
Dziedziną funkcji nazywamy zbiór wszystkich argumentów x, dla których funkcja ta jest określona.
Wyznaczanie dziedziny funkcji
Podczas wyznaczania dziedziny funkcji musimy pamiętać, że:
- dzielenie przez zero jest niewykonalne, w przypadku ułamka mianownik musi być różny od 0,
- liczba podpierwiastkowa nie może być ujemna
- liczba podpierwiastkowa w mianowniku pewnego ułamka musi być liczbą dodatnią
Kiedy wyznaczamy dziedzinę pewnej funkcji, staramy się patrzeć prościej na to, co widzimy. Czyli kiedy zobaczymy taki prosty wzór:

Nasz tok rozumowania będzie wyglądał tak:
- Jest to po prostu ułamek
 , dlatego mianownik (czyli b) ma być różne od zera , dlatego mianownik (czyli b) ma być różne od zera
- Zauważamy, że a = x2. Zastanawiamy się, czy jest tu jakiś ułamek lub pierwiastek, lecz na szczęście nie ma. Zatem w tym przypadku
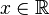
- Patrzymy na mianownik. Mamy b = x + 2. Niestety, ponieważ jest to mianownik (pamiętamy „nigdy cholero nie dziel przez zero!”), musimy założyć, że
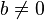 , czyli , czyli  . .
- Na koniec podsumowujemy wszystko. Czyli odrzucamy wszystkie x, które zostały odrzucone w którymś punkcie. Czyli otrzymujemy
 , zatem dziedziną będzie , zatem dziedziną będzie  . .
Zbiorem wartości funkcji nazywamy zbiór tych elementów zbioru Y, którym zostały przyporządkowane elementy ze zbioru X. Zbiór wartości funkcji f będziemy oznaczać przez ZWf.
|
|