|
Wektorem nazywamy parę uporządkowanych punktów. Pierwszy z tych punktów nazywamy początkiem wektora, a drugi jego końcem.
Kierunkiem wektora  . nazywamy prostą, na której leżą punkty A i B. . nazywamy prostą, na której leżą punkty A i B.
Zwrotem wektora  . nazywamy zwrot półprostej AB. . nazywamy zwrot półprostej AB.
Wektor o początku A i końcu B oznacza się:  . .
Wektory oznacza się też małymi literami np.:  . .
Długość (wartość) wektora  jest to odległość między punktami A i B, oznacza się ją symbolem jest to odległość między punktami A i B, oznacza się ją symbolem  (nie może być ujemna) (nie może być ujemna)
Jeżeli A = B to wektor  nazywamy wektorem zerowym. nazywamy wektorem zerowym.
Do obliczenia współrzędnych wektora  można posłużyć się wzorem można posłużyć się wzorem ![vec{AB} = [ x_B - x_A
, y_B - y_A ]](http://upload.wikimedia.org/math/d/0/4/d047af7accb2fd5580e69737ab929b6c.png)
Długość wektora  liczy się ze wzoru liczy się ze wzoru  lub lub ![vec a = [p, q] Rightarrow ; |vec a| =
sqrt{ p^2 + q^2 }](http://upload.wikimedia.org/math/6/8/f/68fb1110782983f445e30048e94263eb.png)
Działania na wektorach
Suma wektorów  i i 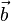
by dodać do siebie dwa wektory należy obrać sobie dowolny punkt O, będący początkiem wektora równego do wektora  , a koniec tego wektora za początek wektora równego do wektora , a koniec tego wektora za początek wektora równego do wektora 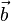 . Wektor, którego początek znajduje się w punkcie O a koniec znajduje się na końcu drugiego wektora nazywamy sumą wektorów . Wektor, którego początek znajduje się w punkcie O a koniec znajduje się na końcu drugiego wektora nazywamy sumą wektorów  i i 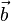
Sumę wektorów  i i 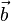 można obliczyć dodając do siebie odpowiednie współrzędne wektorów. można obliczyć dodając do siebie odpowiednie współrzędne wektorów.
![vec a = [a_1, a_2]](http://upload.wikimedia.org/math/9/f/f/9ffe218e8871988376b70ad5d3a626a5.png) i i ![vec b = [b_1, b_2] Longrightarrow vec a
+ vec b = [a_1 + b_1, a_2 + b_2]](http://upload.wikimedia.org/math/9/5/2/952076c99d4dbff7544d9a58f078d062.png) . .
Wzor na srodek wektora : S=(Ax+Bx/2,Ay+By/2)
|